Efficiency (statistics)
In statistics, efficiency is a term used in the comparison of various statistical procedures and, in particular, it refers to a measure of the optimality of an estimator, of an experimental design[1] or of an hypothesis testing procedure.[2] Essentially, a more efficient estimator needs fewer samples than a less efficient estimator to achieve a given accuracy.
The relative efficiency of two procedures is the ratio of their efficiencies, although often this term is used where the comparison is made between a given procedure and a notional "best possible" procedure. The efficiencies and the relative efficiency of two procedures theoretically depend on the sample size available for the given procedure, but it is often possible to use the asymptotic relative efficiency (defined as the limit of the relative efficiencies as the sample size grows) as the principal comparison measure.
Efficiencies are often defined using the variance or mean square error as the measure of desirability.[1] However, for comparing significance tests, a meaningful measure can be defined based on the sample size required for the test to achieve a given power.[3]
For experimental designs, efficiency relates to the ability of a design to achieve the objective of the study with minimal expenditure of resources such as time and money. In simple cases, the relative efficiency of designs can be expressed as the ratio of the sample sizes required to achieve a given objective.[4]
Contents |
Definition
The efficiency of an unbiased estimator T is defined as
where 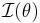 is the Fisher information of the sample. Thus e(T) is the minimum possible variance for an unbiased estimator divided by its actual variance. The Cramér–Rao bound can be used to prove that e(T) ≤ 1.
is the Fisher information of the sample. Thus e(T) is the minimum possible variance for an unbiased estimator divided by its actual variance. The Cramér–Rao bound can be used to prove that e(T) ≤ 1.
Efficient estimators
If an unbiased estimator of a parameter 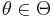 attains
attains 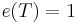 for all values of the parameter, then the estimator is called efficient.
for all values of the parameter, then the estimator is called efficient.
Equivalently, the estimator achieves equality on the Cramér–Rao inequality for all 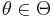 .
.
An efficient estimator is also the minimum variance unbiased estimator (MVUE). This is because an efficient estimator maintains equality on the Cramér–Rao inequality for all parameter values, which means it attains the minimum variance for all parameters (the definition of the MVUE). The MVUE estimator, even if it exists, is not necessarily efficient, because "minimum" does not mean equality holds on the Cramér–Rao inequality.
Thus an efficient estimator need not exist, but if it does, it is the MVUE.
Asymptotic efficiency
For some estimators, they can attain efficiency asymptotically and are thus called asymptotically efficient estimators. This can be the case for some maximum likelihood estimators or for any estimators that attain equality of the Cramér–Rao bound asymptotically.
Example
Consider a sample of size  drawn from a normal distribution of mean
drawn from a normal distribution of mean  and unit variance, i.e.,
and unit variance, i.e., 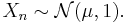
The sample mean, 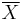 , of the sample
, of the sample 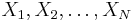 , defined as
, defined as
has variance 1/N. This is equal to the reciprocal of the Fisher information from the sample and thus, by the Cramér–Rao inequality, the sample mean is efficient in the sense that its efficiency is unity (100%).
Now consider the sample median. This is an unbiased and consistent estimator for  . For large
. For large  the sample median is approximately normally distributed with mean
the sample median is approximately normally distributed with mean  and variance
and variance 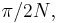 i.e.,
i.e.,
The efficiency for large  is thus
is thus 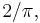 or about 64%. Note that this is the asymptotic efficiency — that is, the efficiency in the limit as sample size
or about 64%. Note that this is the asymptotic efficiency — that is, the efficiency in the limit as sample size  tends to infinity. For finite values of
tends to infinity. For finite values of 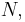 the efficiency is higher than this (for example, a sample size of 3 gives an efficiency of about 74%).
the efficiency is higher than this (for example, a sample size of 3 gives an efficiency of about 74%).
The sample mean is thus more efficient than the sample median. However, there may be measures by which the median performs better. For example, the median is far more robust to outliers, so that if the Gaussian model is questionable or approximate, there may advantages to using the median (see Robust statistics).
Relative efficiency
If 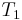 and
and 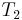 are estimators for the parameter
are estimators for the parameter  , then
, then 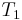 is said to dominate
is said to dominate 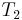 if:
if:
- its mean squared error (MSE) is smaller for at least some value of

- the MSE does not exceed that of
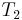 for any value of θ.
for any value of θ.
Formally, 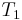 dominates
dominates 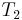 if
if
holds for all  , with strict inequality holding somewhere.
, with strict inequality holding somewhere.
The relative efficiency is defined as
Although  is in general a function of
is in general a function of  , in many cases the dependence drops out; if this is so,
, in many cases the dependence drops out; if this is so,  being greater than one would indicate that
being greater than one would indicate that 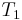 is preferable, whatever the true value of
is preferable, whatever the true value of  .
.
Hypothesis tests
Pitman efficiency[5] and Bahadur efficiency (or Hodges–Lehmann efficiency )[6][7] relate to the comparison of the performance of Statistical hypothesis testing procedures.
Uses of inefficient statistics
There are various inefficient estimations of statistical parameters which can be calculated with far fewer mathematical operations than efficient estimates.[8][9] Before the advent of electronic calculators and computers, these provided a useful way to extract much of the information from a sample with minimal labour. For example, given a sample of a normally-distributed numerical parameter, the arithmetic mean (average) for the population can be estimated with maximum efficiency by adding all the members of the sample and dividing by the number of members. However, the mean can be estimated with an efficiency of 64% or better (depending on sample size) relative to the best estimate by taking the median of the sample, with no calculations required. It can be estimated from a large sample with an efficiency of about 81% (similar methods are available for small samples; there are also more efficient methods using more values) by simply averaging the two values 29% of the way in from the from the smallest and the largest values,[9] vastly less laborious than adding all the members of a large sample. These methods may be of some use even now, e.g. for estimating the mean given a list of numerical values in non-machine-readable form.
See also
Notes
- ^ a b Everitt (2002) p 128
- ^ Nikulin, M.S. (2001), "Efficiency of a statistical procedure", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1556080104, http://www.encyclopediaofmath.org/index.php?title=E/e035080
- ^ Everitt (2002) p 321
- ^ Dodge, Y. (2006) The Oxford Dictionary of Statistical Terms, OUP. ISBN 0-19-920613-9
- ^ Nikitin, Ya.Yu. (2001), "Efficiency, asymptotic", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1556080104, http://www.encyclopediaofmath.org/index.php?title=E/e035070
- ^ Arcones M.A. "Bahadur efficiency of the likelihood ratio test" preprint
- ^ Canay I.A. & Otsu, T. "Hodges-Lehmann Optimality for Testing Moment Condition Models"
- ^ Mosteller, Frederick (1946) On Some Useful "Inefficient" Statistics. Reprinted in: Fienberg, Stephen; Hoaglin, David (Eds) (2006) Selected Papers of Frederick Mosteller, Springer New York. ISBN 978-0-387-44956-2 doi:10.1007/978-0-387-44956-2_4
- ^ a b RD Evans (1955) The Atomic Nucleus, Appendix G: Inefficient statistics
References
-
- Everitt, B.S. (2002) The Cambridge Dictionary of Statistics, CUP. ISBN 0-521-81099-x
External links
- Nikitin, Ya.Yu. (2001), "Efficiency, asymptotic", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1556080104, http://www.encyclopediaofmath.org/index.php?title=E/e035070
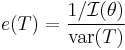
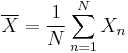
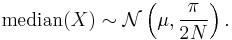
![\mathrm{E}
\left[
(T_1 - \theta)^2
\right]
\leq
\mathrm{E}
\left[
(T_2-\theta)^2
\right]](/2012-wikipedia_en_all_nopic_01_2012/I/372ed8d78dce9eef004a1e6e0c9de3dc.png)
![e(T_1,T_2)
=
\frac
{\mathrm{E} \left[ (T_2-\theta)^2 \right]}
{\mathrm{E} \left[ (T_1-\theta)^2 \right]}](/2012-wikipedia_en_all_nopic_01_2012/I/17e7a0acc6536953ff3053bc1684bf75.png)